determine the legs and the height, h.
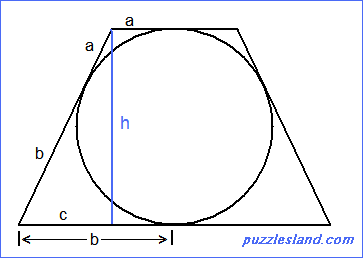 Let A = 2a and B = 2b.
Let A = 2a and B = 2b.If we draw the inscribed circle,
and note that tangents to a circle from a common point are equal,
we see that the legs of the trapezoid
are equal to (a + b) = (A + B) / 2.
If we drop the perpendicular shown in blue, we have c = b - a.
From the Pythagorean Theorem:
(b - a)^2 + h^2 = (b + a)^2
b^2 - 2ab + a^2 + h^2 = b^2 + 2ab + a^2
h^2 = 4ab and h = 2 sqrt(ab)
This is so interesting Ashley! I am honestly like flabergasted at the fact that people can figure this out.
ReplyDelete