Intoduction of Limits

   Definition of Limits: 

• If f(x) becomes arbitrarily close to a unique numeb L as x approaches c from either side, the limit of f(x) as a approaches c is L. 

   Conditions under which Limits do not exist:

• f(x) approaches a different number from the right side of c than from the left side of c
• f(x) incereses or decreases without bound as x approaches c
• f(x) oscillates between tweo fixed values as x approaches c

Techniques for Evaluating Limits

Example of substitution:

Example of factor:

Example of conjugate:

Heights of isosceles trapeziod

Given the bases, A and B, of an isosceles trapezoid,
determine the legs and the height, h. 
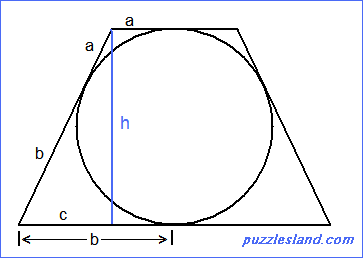Let A = 2a and B = 2b.
If we draw the inscribed circle,
and note that tangents to a circle from a common point are equal,
we see that the legs of the trapezoid
are equal to (a + b) = (A + B) / 2.

If we drop the perpendicular shown in blue, we have c = b - a.

From the Pythagorean Theorem:
(b - a)^2 + h^2 = (b + a)^2
b^2 - 2ab + a^2 + h^2 = b^2 + 2ab + a^2
h^2 = 4ab and h = 2 sqrt(ab)

11.2 Vectors in Space

 Vectors in space can described by ordered triples of coordinates (x,y,z). Geometrically, the vector can be thought of as an arrow pointing from the origin to this point in space.

11.1 The Three-Dimensional Coordinate System

The 3-D coordinate system is formed by passing a z-axis perpendicular to both the x-axis and y-axis at the origin.

x = directed distance from yz-plane to P

y = directed distance frim xz-plane to P

z = directed distance from xy-plane to P

Example: Find the distance between (1, 0, 2) and (2, 4,-3)

5 graph